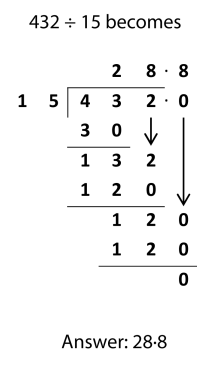
My Year 6 daughter has recently learnt long division. To be clear on what I’m referring to, long division looks like this:
Whereas ‘short division’ looks like this (this is sometimes colloquially referred to as a ‘bus stop method’):
The only difference between the two methods is that in short division we work out the remainders in our head and jot them down in the dividend, but in long division we work out the remainders on paper in a more structured format. If your divisor is greater than twelve (for example if you’re dividing by 28) then it might be tricky to work out remainders in your head, so that’s typically when the long division format might be preferred. But they’re essentially the same method, just with a slightly different structure for processing the calculations.
It was funny to see my daughter learning long division as it’s something that I literally never teach in secondary school. I was pleased with myself for remembering how it works. For many students it exists in Year 6 alone, never to be seen again. A typical Key Stage 2 SATs question might look like this:
But something like this is highly unlikely to come up at GCSE. Students do sometimes have to do divisions by hand in their non-calculator GCSE exam (an example is shown below, from the Foundation tier), but I think most students would choose to use short division.
Some people argue that the long division algorithm is used again when students learn algebraic division in Year 12. This may have been the case ten years ago, but I think that most(?) A level teachers now prefer more intuitive methods of polynomial division, like the factor method shown below for example.
So for the most part, long division resides solely in Year 6. And my daughter, who is in the ‘middle’ group for maths, was coping fine with it, but she told me that she finds it tricky to write out the multiples at the start. For example when she’s dividing by 28, she’s been told to begin by writing out some multiples of 28. She finds this time-consuming, a bit tricky, and rather dull.
But don’t worry, because there’s a really simple way to write out the multiples of 28. My colleague Sian showed me this – she picked it up a few years ago from her daughter’s Year 6 teacher. I showed my daughter, who loved it – she was then able to master long division as she’d found a way round the tricky bit.
To quickly and easily write out the multiples of 28, just write the multiples of 20 and the multiples of 8 and add them together:
As long as the child knows their standard times tables fairly well, listing the two sets of multiples is straightforward. And the addition is pretty straightforward too, as they are always adding to a multiple of ten.
Here’s another example: multiples of 17.
This may already be really widely used by Year 6 teachers. But in case anyone hadn’t thought about this super simple way of listing multiples, I thought it worth sharing here. As I’ve always said, even if it just helps one person then it’s worth taking the time to write about it.